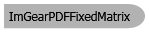
A B 0

C D 0

H V 1

A transformation matrix has only six elements that can be changed as the six-element array [ a b c d h v ]. It can represent any linear transformation from one coordinate system to another. The transformation matrix multiplication can be presented as follows:

x1 = x*A + y*C + H

y1 = x*B + y* D + V

The following lists the arrays that specify the most common transformations:

• Translations are specified as [ 1 0 0 1 tx ty ], where tx and ty are the distances to translate the origin of the coordinate system in the horizontal and vertical dimensions, respectively.
• Scaling is obtained by [ sx 0 0 sy 0 0 ]. This scales the coordinates so that 1 unit in the horizontal and vertical dimensions of the new coordinate system is the same size as sx and sy units, respectively, in the previous coordinate system.
• Rotations are produced by [ cos Ang sin Ang -sin Ang cos Ang 0 0 ], which has the effect of rotating the coordinate system axes by an angle Ang counterclockwise.
• Skew is specified by [ 1 tan a tan b 1 0 0 ], which skews the x axis by an angle a and the y axis by an angle b.

If several transformations are combined, the order in which they are applied is significant. For example, first scaling and then translating the x axis is not the same as first translating and then scaling it.

In general, to obtain the expected results, transformations should be done in the following order:

Translate

RotateScale or skew

See section "4.2 Coordinate Systems" of the PDF Reference for more details.

System.Object
   ImageGear.Formats.PDF.ImGearPDFFixedMatrix

Reference